其实如果我们深入去学习生物信息,最核心根本不是你会不会R,能不能用perl写脚本,或者用最潮最新的python去开发一个新的生信软件。
而是懂算法, 懂原理!
[TOC]
前言
其实如果我们深入去学习生物信息,最核心根本不是你会不会R,能不能用perl写脚本,或者用最潮最新的python去开发一个新的生信软件。
随着不断的工作的积累,慢慢的对自己的工作也多了几分认识。在高通量测序这个行业中的技术支撑,在单纯的技术方面可以分为三个阶段。
- 懂的如何看结果,如何解读结果
- 懂原理
- 懂如何优化结果
但是作为技术支撑,势必是要懂些生信分析,但是同样的生信分析也是分为三个等级
- 会跑流程
- 懂流程的细节
- 懂算法和原理
比如我一直在看的WGCNA文献,其实整体看下来,WGCNA分析是图形难画吗?是涉及什么高深的生物知识吗?其实都不是,反而通篇的如何用图论和算法来进行分析。可以说WGCNA分析其实就是个算法包。详情请看
数据处理
其实今天要说的是关于数据的处理,因为在PCA分析中,pcromp函数主成分的时候,是有三个参数的,其中有两个参数在其他的分析中也是很常见的。在R中函数名称往往是scale和center。以前总是不理解。那是因为没什么必要去了解,但是当自己上台去讲如何用pheatmap绘制热图时,就需要知道了,因为热图绘制中有一个非常重要的参数是scale = "row",也就是对行进行均一化。虽然我也能简单说几句,行均一化是因为可以降低变异范围,将所有基因在同一个范围内方便直观进行比较。其实自己心里明白,这是当支撑久了一种经验上的说法,其实真正的原理自己完全不清楚,禁不起推敲。
因为搜索了相关的资料,第二天在讲课的时候,顺手就做了一个函数,解释了原理。课下的时候也正好被老师问起这些处理,自己把自己的理解讲了一番。也算是学有所用吧。
更多就放在公众号里,记录一下关于数据的预处理的一些认识。
标准化scale
scale处理广泛应用在数据分析中,其本质是将数据特征重新缩放,并且它们将具有标准正态分布的性质(其实我发现如果原始数据不是正态分布,标准化后,还是一样,不会变成正态分布)
所以其实标准化最重要的作用应该是将原本的特征值重新缩放,并且能局限在某个范围,并且这个范围还是一个标准差为1,平均值为0的这样的一个分布范围。更符合数据美学。但其实只是一种特征值缩放的手段。
标准化算法的公式是: $$ z = \frac{x - \mu}{\sigma} $$ 其中u是平均值,sigma是标准差。因为我脑子不够用了,所以没办法用复杂的数学公式来实现计算,是不是真是标准差为1,平均值为0。偷懒的我在R上,自己写了一个函数。来验证一下,果真如此。
# R 3.5.3 win 10
scales<-function(x){
return((x-mean(x))/sd(x))
}
dat <- sample(10000,300)
dat1 <- scales(dat)
as.integer(mean(dat1))
sd(dat1)
d<-density(dat1)
plot(d)
plot(d,main = "数据标准化(scale)")
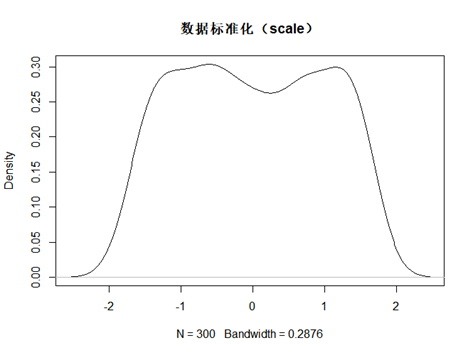
归一化(Normalization)
归一化:把数据变成(0,1)或者(1,1)之间的小数。这样可以将数据的变异范围局限在一定范围,同时保存了数据之间原有的变异度。在某些图像算法和神经网络算法中用的比较多。
归一化处理的算法是: $$ X_{norm} = \frac{X - X_{min}}{X_{max}-X_{min}} $$ 上述的公式还是比较好理解的,就是看特征值在极差范围内的排序。在这种方法中,数据被缩放到固定范围[0,1],作为被限定边界的补偿,得到的是,与标准化相反,归一化最终会得到较小的标准偏差,这可以抑制异常值的影响。
这点我们通过R很容易就可以发现
> Norm <-function(x){
return((x-min(x))/(max(x)-min(x)))
}
> dat2 <- Norm(dat)
> mean(dat2)
[1] 0.516856
> sd(dat2)
[1] 0.2819505
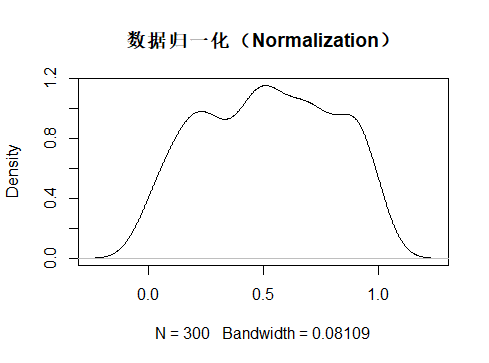
可以看到上述的归一化的标准差sd 要比标准化处理的标准差sd要小很多,这也代表着归一化可以极大的抑制异常值对数据分析的影响。
另外被压缩在固定范围内,对某些神经网络算法和机器学习算法会相应的减少计算量(其实我也不是很懂这些算法,但是机器学习还是了解一点点点点的)
但是一般我们仍然不选择归一化处理,而是优先选择标准化,原因是两者的作用都是压缩特征值,但是标准化可以保留原始数据的变异度,即有利于我们在相对变异小的范围内,进行数据分析。同时也有利于我们发现数据中的问题。而归一化很可能就会掩盖这个异常效应。
这在我们的生信分析中尤为重要,因为生命本身是很复杂的活动,太多的因素会导致数据或多或少的出现异常值。如果我们能发现异常值,就可以有针对性的优化。
没有标准化的流程分析,只有最适合的参数和流程。相信这才是生信分析的个性化所在!
另外归一化还有非线性的归一化,弦函数和log对数处理,这个相信各位能自己写出来这个函数,不如留个小任务,待你去发掘!
中心化(center)
中心化的算法就比较简单了, $$ z = {x - \mu} $$ 就是很简单的特征值减去平均值。这个处理就是压缩数据。但其实更多的是一种特征值变换,就是变成有正负了。实话实话,我不知道这个干嘛,网上资料很少,谷歌也没这么说。并且我自己理解用处也有限。只是降低了平均值,但是数据分布的重要衡量标准—标准差没有任何变化啊。所以我个人猜测中心化只适合一些特定场景下的数据处理。原理这么简单,到时候自己遇到了,就自己用用呗。
也用函数探究一下:
首先是原始矩阵的平均值和标准差,因为我担心中心化处理的效果太弱,只好拿原始数据来做比对。
> mean(dat)
[1] 5168.167
> sd(dat)
[1] 2804.562
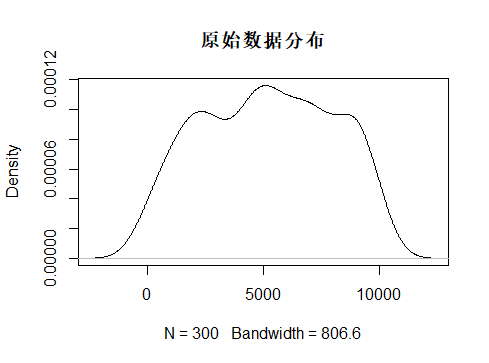
在看看中心化处理后的数据分布
> dat3 <- center(dat)
> mean(dat3)
[1] -3.033596e-13
> sd(dat3)
[1] 2804.562
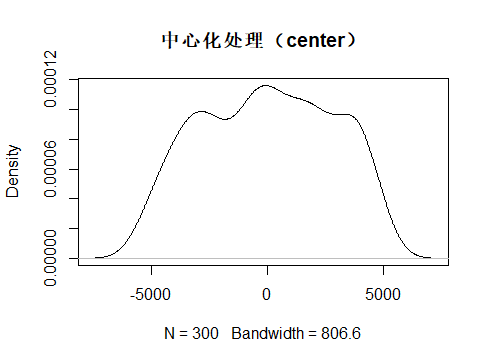
总结
大数据分析,有事没事来个标准化(scales),出现调整不了的异常值,就用归一化(Normalization),线性归一化不行,就用非线性的。
center等你想起来用的时候再用吧。
到此结束,感谢各位关注,谢谢
下期精彩预告: