1. 前言
接触组学多了,感觉分析主要有两类,一个是基于被研究对象的位置和序列。一类是基于算法。前者比如说lncRNA与mRNA的antisense和cis的作用关系,miRNA和piRNA的靶向基因预测等。后者就比如说机器学习、降维、聚类等算法。
其中机器学习是通过程序不断的迭代来寻找合适的模型
降维就是将高维数据通过计算,在尽量保证数据原始分布特征的情况下,将数据映射在低维的刻度。
markdown preview
聚类方法很多,常用的是计算欧式距离后,用K-mean聚类算法进行聚类,K-mean聚类算法就是先随机挑选k个中心,按照距离远近分别聚在一起。然后在聚类的簇里重新选择平均值作为中心点,重新聚类,然后不断迭代设置的次数,最后的结果就是聚类结果。当然如果画树,还涉及分类树的算法。简而言之,麻烦,不详细说了。
相关性分析,这就是本文要详细说的了。
2. 相关性分析
相关性分析是一种统计技术,
相关性分析,就是衡量两个变量之间的依赖性强弱
相关性:可以显示两个变量是否相关以及如何相关。例如,身高和体重是相关的; 较高的人往往有更大的体重。那么这种关系就是正相关。那么再例如汽车排量与每升汽油的里程,是负相关的,汽车排量越大,每升汽油跑的里程就越短。
尽管这种相关性非常明显,但您的数据可能包含未预料到的相关性。您可能还会产生怀疑。怀疑两个变量之间是否存在相关性,或者不知道两者之间的依赖和联系程度。这个时候,就会需要一种可以量化的指数分析。相关分析可以帮助我们更好地理解数据。
但是
使用相关性分析的时候,我们需要记住的一个关键事项是:永远不要假设相关性就一定意味着A变量的变化会导致B变量的变化。多年来个人电脑和运动鞋的销售都强劲增长,并且它们之间存在高度相关性,但你不能认为购买电脑会导致人们购买运动鞋(反之亦然)。但可能还是可能存在相同的调节因素,比如社会生产力的提高和经济状况的改善。
2.1 正负相关性
当两个变量之间存在非常强烈的相互依赖关系的时候,我们就可以说两个变量之间的存在高度相关性。
- 若两组的值一起增大,我们称之为正相关,
- 若一组的值增大时,另一组的值减小,我们称之为负相关

本次我们用R来进行计算和绘图,所用的数据是R自带的mtcars数据
> mtcars
> head(mtcars)
mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
那么行名我们知道是汽车的型号。那么列名呢,
| mpg | cyl | disp | hp | wt |
|---|---|---|---|---|
| 英里/加仑 | 气缸数量 | 排量 | 总马力 | 重量 |
从上述列名中,我们可以简单得到排量(disp)与马力(hp)呈现正相关性,而与每加仑汽油行驶的里程是负相关性。
那么我们就可以用R的cor函数来计算两个变量之间的相关性。
library(ggplot2)
r <- cor(mtcars$disp,mtcars$mpg,method = "pearson")
p1 <- ggplot(data = mtcars, aes(x = disp, y = mpg)) +
geom_point(color = "#d7191c") +
geom_smooth(method = "lm",color = "#1a9641") +
geom_text(aes(x = 400, y = 32,label = paste("R" ,"=",signif(r,3),seq = "")),color ="#fdae61") +
theme_bw()
r1 <- cor(mtcars$disp,mtcars$hp,method = "pearson")
p2 <- ggplot(data = mtcars, aes(x = disp, y = hp)) +
geom_point(color = "#d7191c") +
geom_smooth(method = "lm",color = "#1a9641") +
geom_text(aes(x = 400, y = 32,label = paste("R" ,"=",signif(r1,3),seq = "")),color ="#fdae61") +
theme_bw()
cowplot::plot_grid(p1,p2,nrow = 1,labels = c("p1","p2"),hjust = 0.05)
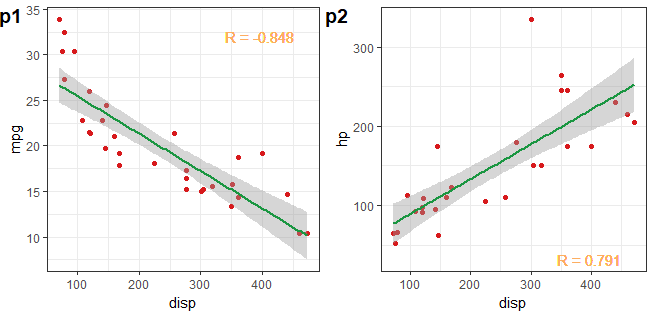
2.2 相关分析的局限
刚刚我们知道了,相关性分为正相关和负相关。但这里,我们之说的是线性相关。因为非线性相关的话,更适合建模拟合多元回归。这个还是很牛的领域,只是我还没涉及,上次去青岛做生信培训,就有老师想构建四因素的多元回归分析。这个领域我完全没有了解。就不说了。
但是用R中cor函数来计算相关性也是有局限的。首先第一点,不能计算非线性模型,
例如我们先看一组简化的数据,icecream是冰激凌的销售额。sunglass是太阳镜的销售额。tem是温度。
sunglass <- c(213,233,296,345,645,644,492,691,790,667,645,546,506,524,434,383,282,181,30,50,30)
icecream <- c(215,236,300,350,651,651,500,700,800,678,657,559,520,539,450,400,300,200,50,30,50)
tem <- seq(30,40,0.5)
dat <- data.frame(sunglass, icecream, tem)
我们先看在温度低于35时候的冰激凌销售与温度之间的关系。
require(magrittr)
dat_low <- dat %>% dplyr::filter(tem < 35)
r2 <- cor(dat_low$icecream, dat_low$tem)
p3 <- ggplot(data = dat_low, aes(x = tem, y = icecream)) +
geom_point() +
geom_smooth(method = "lm", color = "#1a9641") +
geom_text(aes(x = 34, y = 500,label = paste("R" ,"=",signif(r2,3),seq = "")),color ="#fdae61") +
theme_bw()
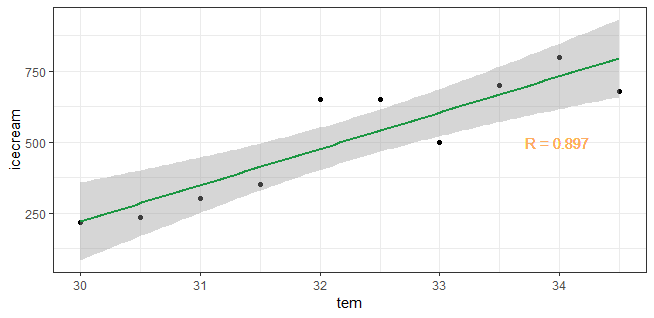
这个时候,我们可以看到当温度低于35度的时候,冰激凌销量是和温度正相关的。但是随着天气炎热,大家都不愿出远门,这时候冰激凌的销售就下来了。温度在30度到40度之间的时候,温度和冰淇淋销量之间的相关性是怎么样呢。
r3 <- cor(dat$icecream,dat$tem)
p4 <- ggplot(data = dat, aes(x = tem, y = icecream)) +
geom_point() +
geom_smooth(method = "lm",color = "#1a9641") +
geom_text(aes(x = 39, y = 500,label = paste("R" ,"=",signif(r3,3),seq = "")),color ="#fdae61") +
theme_bw()
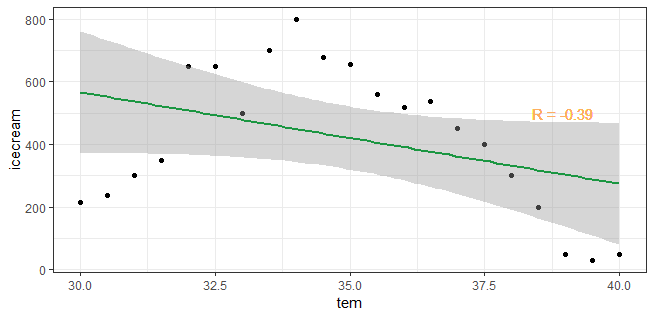
其实我们就可以发现问题,这里的温度和冰激凌销量是有很强的相关性的,我们甚至可以用脑子拟合出一个抛物曲线。虽然这个相关性不是线性的。但是如果我们继续用R中cor函数来计算,用线性相关性分析显然是不正确的。数值才*-0.39*
另外,相关性强,也不等于因果关系。例如我们可以看到太阳眼镜的销量和冰激凌的销量之间的关系。
r4 <- cor(dat$icecream,dat$sunglass)
p5 <- ggplot(data = dat, aes(x = icecream, y = sunglass)) +
geom_point() +
geom_smooth(method = "lm",color = "#1a9641") +
geom_text(aes(x = 700, y = 500,label = paste("R" ,"=",signif(r4,3),seq = "")),color ="#fdae61") +
theme_bw()
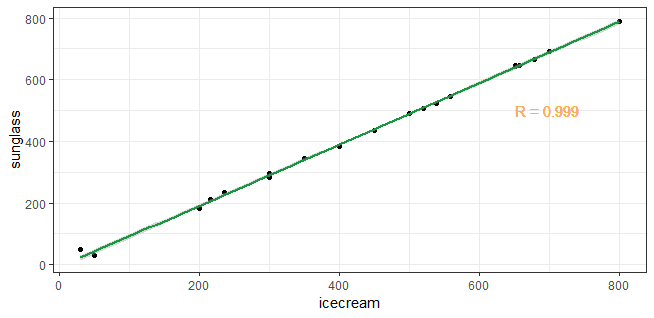
可以看到,就算太阳镜和冰淇淋的销量相关性是0.99,也不能体现两者是因果关系。就是说,相关不代表一个现象导致另一个(相关可能有其他的原因,比如太阳的直射时间)
2.3 相关性计算
cor函数的完整语法如下:
cor(x,y = NULL,use =“everything”,method = c(“pearson”,“kendall”,“spearman”))
也就是说像关系计算,有三种方法,pearson,kendall,spearman三种
2.3.1 pearson相关系数
算法如下:
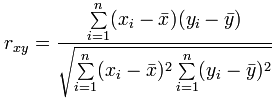
代数算法比较难理解,但分子我们可以看到是个协方差,只是少了除以n-1,而分母是我们很熟悉的标准差,同样少了除以n-1。可以看出分子分母都少了除以n-1,正好抵消。也就意味相关性系数就是协方差除以标准差。
甚至我们可以写成:
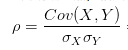
其中cov既是协方差的缩写,也是R中的函数名称。如果想了解这个计公式。我们还要分为三个部分
2.3.1.1 协方差
可以通俗的理解为:两个变量在变化过程中的变化方向是否一致,以及一致的程度。
如果两个变量,A变大,同时B也变大,说明两个变量是同向变化的,这时协方差就是正的。A变大,同时B变小,说明两个变量是反向变化的,这时协方差就是负的。从数值来看,协方差的数值越大,两个变量同向程度也就越大。反之亦然。
公式:
$$
cov(X,Y)=\frac{\sum (x-\overline{x})(y-\overline{y})}{n-1}
$$
如果有X,Y两个变量,每个时刻的“X值与其均值之差”乘以“Y值与其均值之差”得到一个乘积,再对这每时刻的乘积进行求和并求出均值。
首先x减去平均值,就意味着我们将平均值作为一个坐标原点,减去平均值,就意味着。所有的x的取值都会根据这个原点,重新调整数值(位置)。这样我们就可以得到Xn(n = 1,2,3,,,)的变化程度。也就是距离原点的距离远近。这是在x变量中的变化程度。
那么同样y变量中也做这样的取值,得到Yn在Y变量中的变化程度。如果Xn与Yn变化一致。那么要是Xn大于均值,那么X -Xn就是正数,Yn也是同样的,因此这个数是正数。将n依次取每个值。就可以算出X变量与Y变量之间的每个取值时的变化协同性。
以上是理想状态下,实际中,就算X变量与Y变量之间存在协同性,也可能出现,在某个取值的时候,例如当n=2时候,·X2-mean(x) < 0,而·Y2-mean(Y) > 0。但是因为我们是计算每一个取值时的计算结果,最终算一个求和。所以如果X和Y变量存在协同性,那么最终的结果还是为正数。
当然如果x变量与y变量反向相关,计算的结果为负数,代表负相关。
当然,你可能还会想,n = 1,n = 2,n = 3…,每个时刻X,Y都在增大,而且X都比均值大,Y都比均值小,这种情况协方差不就是负的了?7个负值求平均肯定是负值啊?。也就是负相关
但是X,Y都是增大的,明明同向变化的,这不就矛盾了?,当然不矛盾,因为这种情况是不可能的。Xn和Yn减去的是均值。均值既然就意味这肯定有低于均值的Xn和Yn啊。所以结果一定是有正有负,看最后加和后,那方更胜一筹。
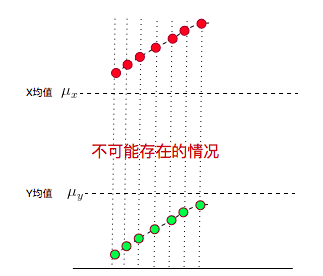
这里,我们知道了协方差是可以衡量两个变量之间的协同变化程度的。
2.3.1.2 标准差
标准差,是我们遇见的,不论是高中的数学课本,还是后面大学和工作遇到的,变异系数,T检验等统计检验值都是需要标准差的。为什么标准差在统计中用到的这么多。
标准差可以衡量数据的分布状况
公式:
$$
\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^N (x_i - \mu)^2}
$$
从公式可以看出,标准差计算方法为,每一时刻变量值与变量均值之差再平方,求得一个数值,再将每一时刻这个数值相加后求平均,再开方。其中Xi - u同样式,以平均值为原点,某一时刻下数值偏离的程度。 取平方值,是因为这个偏离程度有正有负,如果像累加每一个时刻的偏离程度,是需要取一个绝对值,平方是最好的绝对值的方法。
这样累加后,我们就可以得到x变量中数据的整体偏离中心原点的程度。然后我们还需要除以观察时刻的总数,以抵消因为观察次数不同,而产生的影响。因为观察次数越多,求和值肯定越大。所以要除以N。
这里还没完,因为我们之平方取值,所以还需要开平方。
这里我们可以看到:
标准差得到的,变量中数据的分散程度
2.3.1.4 相关性系数
根据上述,我们知道了协方差可以获得,两个变量之间的协同变化程度。标准差可以知道变量的变化范围。
协方差虽然可以衡量变化程度,但是还缺少一个统一的量纲,否则不能进行比较。
例如:
sunglass <- c(213,233,296,345,645,644,492,691,790,667,645,546,506,524,434,383,282,181,30,50,30)
icecream <- c(215,236,300,350,651,651,500,700,800,678,657,559,520,539,450,400,300,200,50,30,50)
cov(sunglass,icecream)
#[1] 54091
cov(((sunglass)*0.01), ((icecream)*0.01))
#[1] 5.4091
p1 <- qplot(sunglass,icecream)
p2 <- qplot(((sunglass)*0.01), ((icecream)*0.01))
cowplot::plot_grid(p1,p2,nrow = 1,labels = c("p1","p2"),hjust = 0.05)
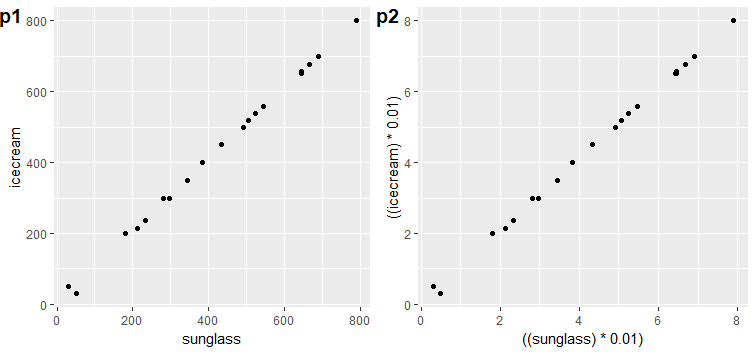
发现问题了吧,明明icecream和sunglass之间是一样的变化协同程度,但是因为波动范围的取值大小,就导致了cov(sunglass,icecream)是54091,而cov(((sunglass)*0.01), ((icecream)*0.01))就变成了5.4091
但是明明是趋势和相关性程度是一致的。这就意味着协方差没有考虑原始数据的分布范围。因此我们还需要将这个值数放在一个量纲下,最好的量纲就是自己的原始数据分布情况。
这不正好需要标准差吗。因此相关性系数的计算就是协方差/标准差
$$
\rho = \frac{\text{cov}(X,Y)}{\sigma_x \sigma_y}
$$
2.3.2 spearman相关性系数
与Pearson相关系数相关,Spearman相关系数测量两个变量之间的关系。Spearman可以理解为Pearson相关系数的基于等级的版本,可以用于非正态分布且具有非线性关系的变量。此外,它的使用不仅限于连续数据,还可用于序数属性的分析。
$$
\rho = 1- {\frac {6 \sum d_i^2}{n(n^2 - 1)}}
$$
是不是感觉有点蒙圈,但其实不难。spearman最大的差别在于,它不是根据原始数值来计算相关性,而是根据排序。
假设两个随机变量分别为X、Y,它们的元素个数均为N,两个随即变量取的第i(1<=i<=N)个值分别用Xi、Yi表示。对X、Y进行排序(同时为升序或降序),得到两个元素排行集合x、y,其中元素xi、yi分别为Xi在X中的排行以及Yi在Y中的排行。将集合x、y中的元素对应相减得到一个排行差分集合d,其中di=xi-yi。
注意区分X和Y的大小些。
我们知道了排名后,其实计算公式还是person那套算法
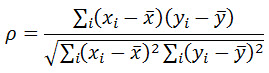
但是我们也可以发现。这样将直接计算排名,会那些非线性的相关性就会非常友好了。此外,还可以适用于非正态分布的数据。但作用也是有限的。不然你试试。
cor(tem,icecream,method ="spearman")
cor(tem,icecream,method ="pearson")
所以至于选择spearman还是选择pearson来计算相关性。这个还要结合数据来说话。因此推荐先用pearson来计算,如果结果不好,就可以试试spearman.
2.3.3 cos余弦相似性
余弦相似性测量两个n维样本向量的方向,而与其大小无关。它由两个数值向量的点积计算,并且通过向量长度的乘积进行归一化,因此接近1的输出值表示高相似性。
$$
cos(\pmb x, \pmb y) = \frac {\pmb x \cdot \pmb y}{||\pmb x|| \cdot ||\pmb y||}
$$
2.3.4 Kendall相似性
和Spearman相关系数类似,Kendall计算排序变量之间的依赖关系,同样适用非正态分布数据。Kendall 可以计算连续数据和有序数据。Kendall在已有排名变量的背景下,通过对错位的强烈惩罚来区别于Spearman的。
公式: $$ \tau = \frac{c-d}{c+d} = \frac{S}{ \left( \begin{matrix} n \ 2 \end{matrix} \right)} = \frac{2S}{n(n-1)} $$
就是如果Xi与Yi的排序是一致的,就会得分,不一致就会减分。其中原理懒的深入,反正用的少。
3. 参考文献
参考资料:
[1] http://blog.sina.com.cn/s/blog_6aa3b1010102xkp5.html
[3] http://www.hep.ph.ic.ac.uk/~hallg/UG_2015/Pearsons.pdf